威布尔分布Weibull在轴承寿命试验研究中的应用

在轴承失效分析研究领域，威布尔分布(Weibull Normal Distribution)有着非常重要的地位。下面简单介绍：

1. 描述寿命分布的三阶段模型

威布尔分布之所以适合轴承，是因为它的形状参数 β 可以直观地反映轴承在不同阶段的失效模式。这完美契合了机械设备典型的”浴盆曲线”寿命特征：

• 早期失效期 （β<1）：主要由于制造缺陷、安装不当或材料瑕疵引起。曲线显示失效率随时间下降。
• 偶然失效期 （β=1）：相当于指数分布，失效率恒定，通常由随机的过载或意外事件引起。
• 磨损老化期 （β>1）：这是轴承最常见的阶段。随着时间推移，疲劳、磨损、电侵蚀等累积效应导致失效率上升。

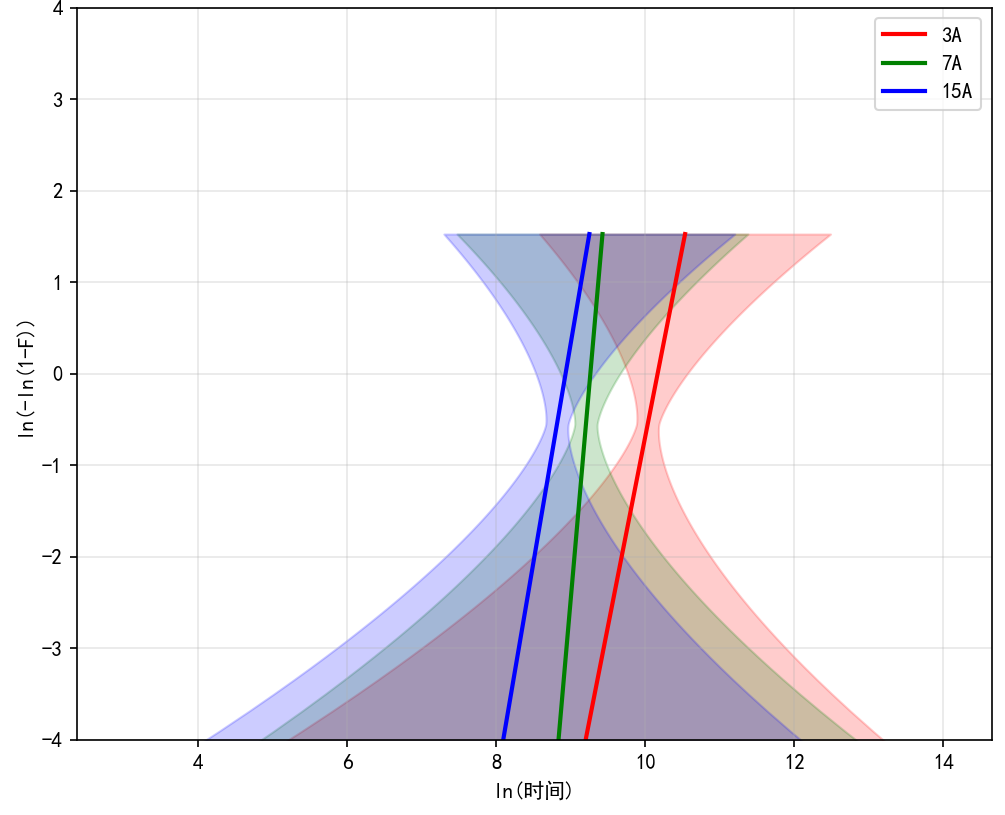
图1：威布尔分布Weibull示例图

2. 加速寿命试验的数据分析核心

在进行加速寿命试验时，威布尔分布是连接”应力”与”寿命”的桥梁。

• 验证加速应力的有效性：加速寿命试验有一个基本假设：在高应力下，轴承的失效模式与正常应力下相同。如何验证这一点？通过比较不同应力水平下的威布尔形状参数 β。
  • 例如β 值在统计上没有显著差异，就说明高应力只是加速了损伤过程，但没有改变损伤的本质。某些研究通过”似然比检验”验证这一假设，使得加速试验的结果可以外推至正常使用条件。
• 建立应力-寿命模型：威布尔分布的尺度参数η（特征寿命）会随着应力水平的变化而变化。通过建立 η与应力之间的关系模型，就可以预测轴承在任意应力下的寿命。

3. 量化关键可靠性指标

威布尔分布可以用来计算轴承可靠性评估中几个最关键的指标：

• 特征寿命 （η） ：指有63.2%的轴承失效的时间点，是衡量产品整体寿命水平的重要基准。
• B10寿命 （L10​）：这是轴承行业最核心的指标之一，指有10%的轴承发生失效的时间（即90%的轴承可靠运行的时间）。
• 平均故障时间 （MTTF）：虽然不如B10常用，但也是衡量平均寿命的重要参考。

4. 工程实践中的具体应用场景

在实际的轴承研发和质量控制中，工程师会这样应用威布尔分布：

• 可靠性验证：新开发的轴承，需要通过台架试验收集失效数据，用威布尔分布拟合，判断其B10寿命是否达到设计要求。
• 工艺改进对比：对比改进前后轴承的威布尔概率图。如果改进后，分布整体右移（η变大），说明平均寿命提高；如果分布变得更陡峭（β变大），说明寿命一致性更好，失效更集中。
• 维护策略制定：根据现场的轴承失效数据，拟合威布尔分布。如果 β>1，说明设备正在进入磨损期，可以计划开始预防性维护；如果 β突然变大，说明可能存在某种新的、更严重的失效模式（如润滑不良或电侵蚀加剧）。

5. 威布尔分布图示示例

图1是一个参考示例，三条直线的斜率就是威布尔分布的形状参数 β。而两侧类似双曲线的形状区域是置信区间，由于置信区间经过了坐标轴对数变换，所以呈现这样的形状。两侧开口大代表不确定性大。